Boyle's Law:

This article describes and defines Boyle's Law with examples of using Boyle's Ideal Gas Law to explain what happens to air in a water storage tank, LP gas in a gas tank, oil & fumes in an oil storage tank, or air conditioning /heat pump refrigerant liquid & gas volumes inside of an air conditioning or heat pump system.

Definition & Practical Applications of Boyle's Gas Law

Boyle's Ideal Gas Law explains the relationship between gas pressure and volume:

P₁V₁ = P₂V₂ all

(P=Pressure V=Volume) at constant temperature

Or stated in simple words, in a closed container containing a gas (air, LP gas, refrigerant, or other), the pressure of the gas times the volume of the gas equals and remains a constant (as long as temperature is also held constant).

For example, in a closed container of refrigerant, if we doubled the volume of the container the pressure of the gas contained therein would be halved from the original container.

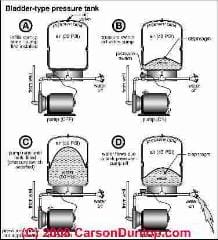
How Boyle's Law Describes How Water Tank Air Volume Changes With Pump Pressure

Continuing a discussion we began at WATER TANK PRESSURE CALCULATIONS, we can re-examine the calculation of variation in water tank air volume in more detail using Boyle's Law.

Boyles Law:   P₁V₁ = P₂V₂  at constant temperature tells us how the volume of a gas changes with changes in pressure, or vice versa, how the pressure of gas changes if we change its volume.

Turning on the water somewhere in the system, we run all of the water out of the tank. (This is not what happens in normal water pressure tank operation. Normally the water pump comes on before all of the water has been pushed out of the water tank. We are using all of the water in this example for simplicity and to describe the absolute maximum amount of water that could be taken out of a water pressure tank.

What happens in the water tank as we run out its water completely? The water volume in the tank goes from 10 gallons to zero. The air volume in the tank goes from 20 gallons to 30 gallons. (Or if you prefer we can convert all of these gallons to cu. ft. - the equations don't care)

What happens to the air pressure during this change? We can work in gallons or cu. ft. of volume.

[Note: We're discussing relative pressure changes within the water tank and piping system; we are not considering the effects of the atmosphere (which is another 14.7 psi at sea level) In a fully-enclosed water tank and piping system the pressures produced by the water supply or water pump should not be significantly affected by atmospheric pressure. ]

20g x 50 psi = 30g x ? PSI solving for PSI = (20x50)/30 = 33 psi

Now in the tank we have 30 gallons of air (or 4 cubic feet of air) at 33 psi. and we have 0 gallons of water with a tank bottom pressure at the water outlet = the air pressure in the tank = 33 psi.

At this point the pump comes back on and pushes water back into the tank.

As water enters the tank bladder it expands the bladder and takes up room in the tank, compressing the air in the tank from 33 psi. back up to 50 psi (the pump cut-off point) and back to our original 20 gallons of air at 50 psi and occupying 2.67 cubic feet and 10 gallons of water being pressed-on with 50 psi of force and occupying 1.33 cubic feet.

Boyles Law in the Water Pressure Tank

A strictly accurate use of Boyle's law would also consider that the pressures we see on a water tank pressure gauge are not absolute pressure which is what Boyle works with but rather, relative pressure - that is, when a water tank pressure gauge reads "0" psi, it has been calibrated for sea level on earth, where the normal air pressure is about 14.7 psi.

This 14.7 psi is the "weight" of the atmosphere pressing down at the earth's surface, per square inch.

So to comply with a strictly correct use of Boyle's law, we'd add 14.7 psi to our water tank pressure gauge readings to get absolute pressure.

When our water tank (at sea level) pressure gauge reads 50 psi, the true absolute pressure in the tank is (50 + 14.7) 64.7 psi. However for switching a water pump on and off, we don't care about absolute pressure, we just care about the pressure change in the system.

That is, when the pressure inside the pressure tank drops from 50 to 30 psi for an absolute pressure drop of 20 psi, the switch needs to turn on the pump. If we calld it a drop from 64.7 psi down to 34.7 psi, the 20 psi change would still be the key figure.

Let's see what happens when we use absolute pressures and then repeat the Boyle's Law calculation performed above:

For a water tank whose pump turns on at gauge pressure of 30 psi and off at gauge pressure of 50 psi, the absolute pressures (adding 14.7 psi for one atmosphere at sea level) will be 44.7 psi and 64.7 psi respectively.

Using our example of pretending that we can take all of the water out of the water tank (0 or now 14.7 psi when the tank is "empty" of water) and that we then pump water back in to a pressure of 50 psi, and using a water tank with a 10 gallon internal volume which will be occupied by some volume of water and air when the pump cycles off:

Tank Volume = 10 gallons = Water Volume + Air Volume

Tank Volume = 10 gallons = 0 gals Water + 10 gals Air (at 0 gauge pressure or 14.7 absolute pressure) when the tank is empty

Let's now pump in water until our water tank pressure reaches 50 psi (gauge) or 64.7 psi (absolute pressure)

Tank Volume = 10 gallons = W gals Water + A gals Air

Using basic algebra, W gals Water = 10 gallons - A gals Air

The air volume in the tank has changed to 10 gallons at 14.7 psi to A gallons at 50 psi.

Using P₁V₁ = P₂V₂, we have (adding the atmospheric pressure at sea level)

(14.7 psi x 10 gals) = ((50 + 14.7) psi x A gals) (just looking at the change in air volume)

(14.7 x 10) / 64.7 = A gals of Air or 2.27 gallons at a gauge reading of 50 psi or an absolute pressure of 65.7 psi.

Our air, compressed from 10 gallons at 14.7 psi to the new pressure of 64.7 psi will now occupy just about 2.3 gallons of volume.

Thanks to reader Bill for careful technical editing, September 2015. - Ed.

Finally! How much space will be occupied by water in our 10 gallon tank?

10 gallons of air compressed down to 3 gallons of air, letting in (10-3) or 7 gallons of water. We have 7 gallons of water in the 10 gallon water tank when the pump shut off at 50 psi.

Now let's adjust our calculations to account for the normal operating range of a water pressure tank and water pump that turns on at 20 psi and off at 50 psi.:

At 50 psi (gauge) in our 10 gallon water tank we have 7 gallons of water and 3 gallons of air.

At 0 psi (gauge) in our 10 gallon water tank we have 0 gallons of water and 10 gallons of air (at 0 gauge or 14.7 psi absolute pressure)

At 20 psi what are our water and air volumes?

Air: (14.7 psi x 10 g) = (20 psi x A gals) or (14.7 x 10)/20 = 7.35 gals of air which leaves (10 - 7.35) = 2.65 gals of water. So at 20 psi we have 7.35 gallons of air and 2.65 gallons of water in the pressure tank, and at this point the pump comes back on to send in more water.

So what is the draw down volume of water in a 20-50 psi 10 gallon water pressure tank? We subtract the 20 psi water volume (2.65) from the 50 psi water volume (7.00) and we get (7.00 - 2.65 = 4.35).

So the draw down volume of water in a 10 gallon water pressure tank operating between 20 psi and 50 psi will be just 4.35 gallons!

...

---

---

ADVERTISEMENT

---

---

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

Reader Comments: for absolute pressure calculations remember the effects of atmospheric pressure too

26 August 2015 Bill said:

Correct me if I am wrong please. For your calculations using 50 psi and 20 psi, aren't they gauge readings which would also need 14.7 psi added to bring them to absolute pressure?

In that case, I get 7.73 gallons at 50 psi gauge and 5.76 gallons at 20 psi gauge giving a difference of only 1.96 gallons instead of 4.41 gallons.

If you really meant 20 psi absolute, then the gauge pressure would only be 5.3 psi which I think is not enough pressure in the house.

Reply:

Bill

Thanks so much for careful reading and questioning. You're right that if we are discussing absolute pressure we need to add the atmospheric pressure to the gauge pressure. I appreciate the thoughtful editing and that you took the time to comment. Working together makes us smarter.

In the article above we comment that

A strictly accurate use of Boyle's law would also consider that the pressures we see on a water tank pressure gauge are not absolute pressure which is what Boyle works with but rather, relative pressure - that is, when a water tank pressure gauge reads "0" psi, it has been calibrated for sea level on earth, where the normal air pressure is about 14.7 psi.

This is the "weight" of the atmosphere pressing down at the earth's surface, per square inch.

So to comply with a strictly correct use of Boyle's law, we'd add 14.7 psi to our water tank pressure gauge readings to get absolute pressure.

However for the purpose of turning on a water pump, we don't care if the pressures are expressed as relative or absolute - we care about the pressure change inside the water pressure tank while water is being run.

For a 20/40 psi pressure control switch, we want to turn the pump ON when pressure falls to or below 20 psi and turn the pump off when the pressure reaches 40 psi - what's key is that 20 psi delta or change - that's the key control interval and it's not changed if we convert all of our pressure settings from relative to absolute.

Question:

(Sept 2, 2015) Bill said:

. I read your reply and the edit you made to the article. But I notice you didn't change the calculations.

So I'm not sure if you understood my comment fully. Sorry if I'm wrong about that. I noticed that you added 14.7 psi to the 0 psi gauge reading in your calculation but you didn't also add the 14.7 psi to the 50 psi (or the 20 psi) gauge reading. I think that is necessary. So the portion of your calculations that show as

(14.7 psi x 10 gals) = (50 psi x A gals)
(14.7 x 10) / 50 = A gals of Air or 2.94 gallons

should really show as

(14.7 psi x 10 gals) = ((50 + 14.7) psi x A gals)
(14.7 x 10) / 64.7 = A gals of Air or 2.27 gallons

and similar for the 20 psi gauge calculation.

Reply:

Right. Thank you.

The questions & answers below, discussing Boyle's Law, were posted originally at this BOYLE's LAW article.

Question: why does water tank pressure slowly fall down from 40 psi when the pump stops to a stable 35-36 psi?

(Oct 9, 2015) Bill said:

I have a question. My tank pumps up to 40 psi, but then it slowly "relaxes" to 35 or 36 psi and then stabilizes there. Why could this be?

... [additional text moved as explained below]

Reply:

Thanks for the interesting question. I've seen this discussed before without an authoritative scientific explanation.

Our best guesses at diagnosing this problem, along with a copy of a more-detailed reply to your own question, can be read at WATER PRESSURE FALLS BRIEFLY THEN STOPS

...

Continue reading at CHARLES' LAW or select a topic from closely-related articles below, or see our complete INDEX to RELATED ARTICLES. or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see this

Gas Pressure Article Series

• BLEVE EXPLOSIONS
• GAUGE, REFRIGERATION PRESSURE TEST
• GAS LAWS & CONSTANTS
  • BOYLE's LAW
  • CHARLES' LAW
  • COMBINED GAS LAW
  • REFRIGERANT PRESSURE READINGS & CHARTS
  • WATER PRESSURE TANK LAW
• OIL TANK PRESSURE
• OPERATING TEMPERATURES HVAC
• PRESSURE CONTROLS & SAFETY SWITCHES
• REFRIGERANT GASES & PIPING
• WATER TANK AIR PRESSURE ADJUSTMENT
• WATER TANK PRESSURE CALCULATIONS

Suggested citation for this web page

BOYLE's LAW at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to AIR CONDITIONING & HEAT PUMPS

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---