InspectAPedia®   -   Search InspectApedia

Roof slope definitions and illustrations (C) Carson Dunlop Associates Roof Calculations of Slope, Rise, Run, Area
Home: How are roof rise, run, area or slope computed?

Roof slope, pitch, rise, run, area calculation methods are explained on this page.

This article series gives easy-to-understand examples of just about every possible way to figure out any or all roof dimensions and measurements expressing the roof area, width, length, slope, rise, run, and unit rise in inches per foot.

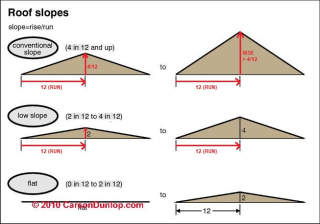
Page top sketch of various roof slopes is provided courtesy of Carson Dunlop Associates, Toronto.

InspectAPedia tolerates no conflicts of interest. We have no relationship with advertisers, products, or services discussed at this website.

- Daniel Friedman, Publisher/Editor/Author - See WHO ARE WE?

How to Calculate the Roof Slope (or any slope) Expressed as Rise & Run from Slope Measured in Degrees: fun with tangents

The slope or pitch of a roof, stair, walk, etc. can be expressed as a number of inches of vertical rise per foot or 12 inches of horizontal travel or run (C) Daniel Friedman at InspectApedia.com

Article Contents

Standard Expression of Roof Slope

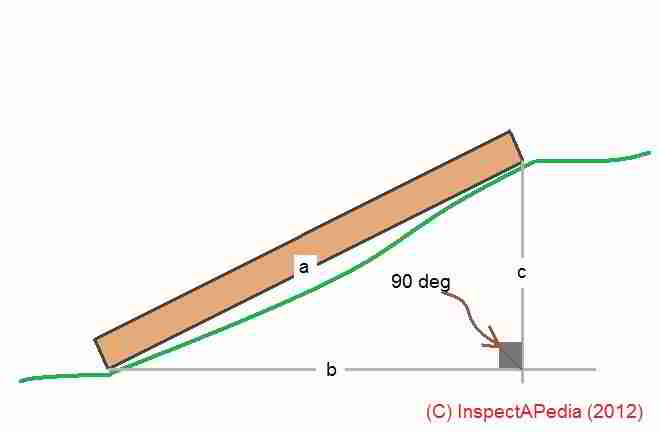
The most common way we describe the slope of a roof is in inches of rise per foot of horizontal distance run. In our sketch above we show three imaginary "steps" up a slope. Each step has a horizontal travel or run distance of X and a vertical rise or increase in height of Y.

We usually write slope or pitch of a roof, stair, or other sloped feature like a ramp as: (inches of rise) / (inches of horizontal run)

or

For example, a 4/12 roof means that the roof height rises 4 inches for every 12 inches of horizontal distance or "run" from the roof edge or eaves towards the roof peak or ridge.

We can measure the rise of a roof directly using simple tools like a level and a measuring tape, or we can convert other slope or pitch measurements into a rise in inches per foot of run, as we'll list next.

[Click to enlarge any image]

Other Expressions of Slope or Pitch

Roof slope (or any slope for that matter such as stairs, ramps, or a hillside) can also be expressed in degrees of angle or in percent slope.

How do We Figure the Total Height or Total Rise of Roofs, Ramps, Roads or Stairs?

For a roof, the total rise is the vertical distance under the ridge to the attic floor. This height tells us how wide we can build an attic room and still have decent head room.

If we know the roof angle or slope and the building width or ramp or stair length or run we can easily calculate the total rise or height, as we'll explain here.

For a stairway, the total rise is the vertical distance between the lower and upper walking surfaces joined by the stairs and the stairway run is the horizontal distance occupied by the stairway.

That calculation is detailed

at CALCULATE ROOF HEIGHT from SLOPE & RUN or BUILDING WIDTH

Use Simple Arithmetic to Convert Percent Grade to Angle or Slope

Measuring the slope of a stair, walk, roof or anything and converting to percent grade (C) Daniel Friedman

Grade, a figure used in road building, is simply a synonym for pitch, slope or angle expressed as a percentage.

Rise / Run x 100 = Slope in Percent

Example:

If I build a sidewalk up the slope of a hill, the building department wants to know if I should have built stairs instead. If the slope, expressed in percent or percent grade is too steep, walkers are likely to slip, fall, and end this discussion.

Suppose my sidewalk is 100 feet long and that the total rise from the low end to the high end of the walk is four feet:

4 ft. / 100 ft. x 100 = 4% Grade - which my inspector accepted as okay. Typical building codes specify that

For pedestrian facilities on public access routes, the running grade of sidewalks will be a maximum of 5%.

By "running grade" we mean that at no point in the sidewalk will the grade be steeper than 5%. In case it's not obvious, that means we'd see a 5 foot rise in100 feet of horizontal travel if the walk were sloped uniformly over its entire length.

Convert Slope or Angle in Degrees into Distance Rise or Run

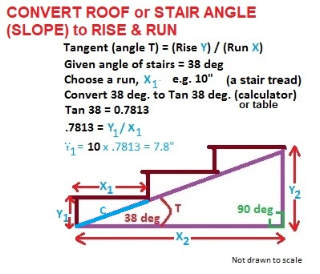How to convert a stair aingle to rise & run using tangent (C) Daniel FriedmanExample: if a roof slope is 38 degrees: what is the rise per foot or 12 inches of horizontal distance or "run"?

When we are describing a roof slope, we normally give the slope as some number of inches of rise (increase in height) for every foot or 12 inches of run (horizontal distance traveled).

But sometimes an annoying architect or engineer or other troublemaker may give us the roof slope in angular degrees such as in this example: 38 degrees.

How do we convert angle in degrees to rise in inches per foot of horizontal run?

Simple tricks with tangents get the roof, stair, road, or walk built to a specified slope

We can quickly convert any slope measured in degrees (or angle) using the basics of plane geometry.

All the magical trigonometry functions of tangent, cotangent, arctangent, sine, cosine, follow from basic geometry.

In our drawing above

X = the unit of horizontal run or one foot or 12 inches

Y = the rise in inches per foot of horizontal run - this is the number we're looking for.

We start knowing three things

  1. X is 12 inches - the number of inches in a foot of horizontal "run" for our roof
  2. The sharp or acute angle formed by lines XC of the right triangle is 38° - this is the slope of our roof in angular degrees.
  3. The right angle at the intersection of lines XY is 90° - a right triangle.

How the heck are we going to find the height of Y - our roof rise per foot of run?

Answer: a 38° sloped roof will have a rise of 9 3/8" per foot of horizontal run. How did we figure that?

We'll use the tangent function provided by geometry.

The tangent of an angle of a roof slope can be calculated as rafter or roof rise divided by rafter or roof run or

Tan (tangent) 38° = Y / X

We could actually calculate the tangent value for an angle, as we explain

at CALCULATE the TAN VALUE from TWO SIDES of a TRIANGLE

Or easier, we can use an online table of Sine/Cosine/Tangent values OR you will find a simple table of these values

at TANGENT CALCULATION or TANGENT TABLE

There we can read:

Tan (tangent) 38° = 0.7813

So we can write

Y / X = 0.7813

and solve for Y, our "rise" per foot of run.

We know that X is 12 inches. We want to calculate Y in inches.

Y (inches of rise) / 12 (inches of run) = 0.7813

Multiply both sides by 12 to get rid of that divisor of 12 on the left:

Y = 12 x 0.7813

Y = 9.375"

So our roof rise per foot of run for a 38 degree sloped roof is 9.375 inches.

Complete details about converting slope or angle to roof, road, walk or stair rise & run along with other neat framing and building tricks using triangles and geometry are found

at FRAMING TRIANGLES & CALCULATIONS.

And for a special use of right triangles to square up building framing,

also see FRAMING SQUARE UP 6-8-10 RULE

Calculate Roof Height Over an Attic Floor From Roof Slope & Building Width

How to calculate roof height at ridge given roof slope & building width (C) Daniel Friedman

[Click to see an enlarged, detailed version of any image]

In geometry, we learned that if we know the lengths of sides of a triangle, we can calculate its angles.

If we know two of its angles, we can calculate the lengths of its sides.

And for a right triangle, the Tangent function gives some easy calculations of an unknown rise or run if I know the other two figures - the angle and either rise or run distance.

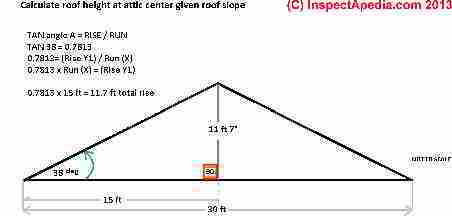
The slope of our example roof is given as 38 degrees.

And we figure that in calculating (or measuring) the "rise" of this same roof, we can assume we are not so stupid as to not hold our tape vertical between the attic floor and the center of the ridge - so we can assume the other known angle is 90 degrees - we've got a nice "right triangle".

If my building width = 30 feet (chosen just for example), how much space do I have overhead in the center of the attic? Since our ridge is over the center of the attic that's the high point.

(Total building width / 2) = (30ft / 2) = 15 ft. total run or total horizontal distance from eaves to attic center under the ridge.

0.7813 x 15 ft = 11.7 ft total  rise across fifteen feet to the highest point in the attic.

Even if I'm Wilt the Stilt Chamberlain I can stand up in the center of this attic. I'm just six feet tall. Never mind Wilt, how far can I walk towards the eaves before I whack my head? We re-use the formula 0.7813= (Rise Y1) / Run (X) as follows?

0.7813 = (6 ft) / X where X is the run distance from the eaves to where I will whack my bean. Rearranging using rules of algebra:

0.7813 x X = 6 ft

X = 6 ft. / 0.7813 = 7.6 ft. 

At 7.6 ft. (that's about 7 ft. 7 in. when we convert decimal feet to inches), I can walk 7 ft. 7 in. from under the ridge before I need a band-aid.

Doubling that, I know we can build a room that is 14 ft. 14 in. which equals 15 ft. 2 in. wide and still have six feet of head room. Neat, right?

Calculate Roof Rafter Length from Slope & Rise

Moved to CALCULATE RAFTER LENGTH from SLOPE & RISE

Table of Roof Slopes, Roof Types, Walkability

This table has moved to a new page at ROOF SLOPE TABLE, TYPES, WALKABILITY

Definition & Uses of Tangent & Tan-1

Moved to DEFINE & USE TANGENTS for SLOPE of ROOFS, STAIRS, WALKS etc

Find the Tangent using a Calculator or a Table

Moved to CALCULATE the TAN VALUE from TWO SIDES of a TRIANGLE

and to TANGENT CALCULATION or TANGENT TABLE

...


ADVERTISEMENT



Reader Comments, Questions & Answers About The Article Above

Below you will find questions and answers previously posted on this page at its page bottom reader comment box.

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

On 2023-08-10 by Kelly - for a 5/12 slope roof on an 18 foot roof what is the building width?

With 18’ metal roofing and wanting a 5-12 pitch,
How WIDE will the building be

On 2023-08-10 by InspectApedia Publisher - How WIDE will a building be given the roof slope calculation?

@Kelly,

Thank you for the roof calculation question.

Using our simplest formula for a right triangle c2 = a2 + b2 where c2 is the sloped line of your roof, a2 is the roof height at ridge and b2 = the roof horizontal run, also = half the building width,

And if I assume that the 18' dimension you cite is the total length of the sloped roof line (c) then we can calculate as follows:

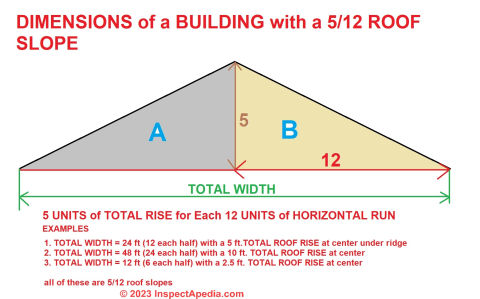
A 5/12 roof will have a total rise of 5 units per every 12 units of horizontal run.

If we write A = total rise, B = total horizontal Run, and C = the sloped line of the roof, we can write

A2 + B2 = C2

For a 5/12 roof we can write

(5)2 + (12)2 = C2

or

25+144 = C2

169 = C2

and taking the square root of both sides

C = 13

that is, for every foot (12") of horizontal run on a 5/12 roof, the length C of the actual roof surface will be 13".

Now if we accept that your roof dimension C is 18 ft. we can divide that in inches (18 x 12 = 216") by 13" (the C-length per foot of horizontal run) to calculate the actual half-width of the building.

216/13 = 16.61 ft. = half the building's width

If your building is a symmetrical A-gable roof shape like in our drawing, then its total width will be 16.61 x 2 = 33.22 ft.

See CALCULATE ROOF HEIGHT from SLOPE & RUN or BUILDING WIDTH

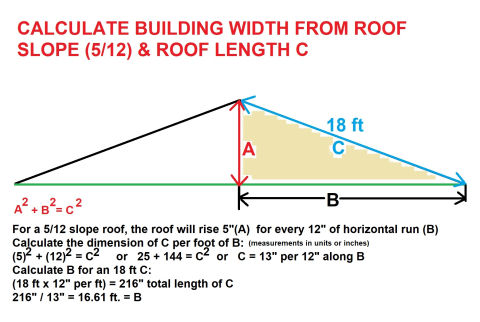
5/12 roof slope calculationsd (C) InspectApedia.com DJF

Illustration of a 5/12 roof showing calculation basics

For other readers, here is a more-general illustration of a 5/12 roof showing calculation basics.

dimensions of a 5/12 roof slope (C) InspectApedia.com DJF

 

On 2023-07-22 by bruce - making a tent: what's the best height and slope?

I am making a tent out of old billboard vinyl stretched between 2 trees, supported by steel cable at the fold

Tent in 48ft x 36 Ft material laying flat.

I am making a rain catchment roof to collect rain water.

I want to fold in half, 18 ft each side of tent.

Trying to figure the rise and best height for the tent fold to allow as much surface area, but also area underneath.
Any suggestions on what I should make the rise height based on these measurements for the water catchment roof.

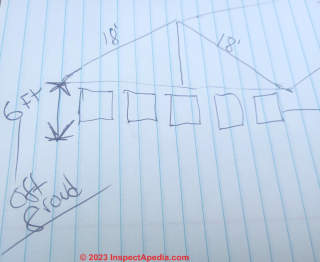
billboard vinyl tent dimensions (C) InspectApedia.com Bruce

On 2023-07-23 by InspectApedia Publisher - best rise and height for the tent made from billboard vinyl

@bruce,

A couple of thoughts: if your two 18 foot widths are already given, you simply choose a building width that gives you as low a slope roof as you can support; keep in mind that as you make the building wider and the roof lower, you may need to make the structure stronger.

At CALCULATE ROOF HEIGHT from SLOPE & RUN or BUILDING WIDTH

you'll see the calculations you can try.

Watch out: if you're planning to collect rainwater running off of this roof and then to use it for human or animal consumption in any form, you might first want to check the chemistry of the old billboard vinyl and its coatings - water running off of such a surface could contain harmful chemicals.

On 2023-05-22 by Ahmed El-Masry - height of a tent attached to a wedding hall building

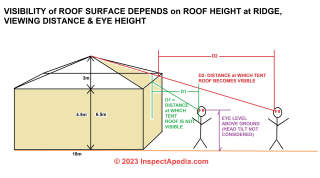
for a wedding hall done by a tent supported by a steel structure, span is 18 m, external height is 4.5 m, center height is 6.50 m, is the slope visually fine from architectural stand point?

On 2023-05-30 by InspectApedia Publisher - at what height does the slope of a roof or tent top become visible?

@Ahmed El-Masry,

Thanks for an interesting question that I'd re-state as "at what height does the slope of a roof or tent top become visible?"

I'm re-stating because I don' t understand what you mean by "visually fine from an architectural standpoint". After all, some buildings have flat roofs that can not be viewed from ground level at any near-level distance and I'm not aware of a definition of "visually fine from an architectural standpoint".

In general, in architecture, "views" are considered a lightweight specification, and there is not one single viewpoint; rather different views take on different importance for different stakeholders.

You will see in my sketch of your wedding hall tent that the visibility of the tent roof depends on the eye level of the viewer, the height of the roof at its peak, and the distance from the tent at which the viewer finds herself.

roof surface visible distance (C) InspectApedia.com DJF


On 2022-05-03 by BENEDICT MOKAYA SIMBA - how many metal roof sections will I need for a building of given size?

How many iron sheets shall be needed in a house measuring 51 ft by 39 ft.

On 2022-05-03 by Inspectapedia Com Moderator

@BENEDICT MOKAYA SIMBA,

I'll be glad to help you do the calculations but it's not possible to answer your question from just the square area of the house.

You have to decide on the roof slope - having a slope means more sheets are needed

And you have to specify the roofing product, such as corrugated steel roofing panel dimensions.

The metal roof panel below, shown as an example, covers 36" wide x 12 ft. long (though ends also must overlap)

metal roof panel example


On 2021-11-12 by Anonymous - calculate rafter length from roof height and slope

The angle of elevation of a roof top is 32°. If the vertical change in height is 4 feet 9 inches as indicated, how long must the rafter be

On 2021-11-12 by Inspectapedia Com Moderator

@Anonymous,

thank you for a helpful question - please find your question and our detailed reply now at

How to CALCULATE RAFTER LENGTH from SLOPE & RISE

https://inspectapedia.com/roof/Roof-Rafter-Length-Calculator.php

and let me know if that leaves you with questions

On 2020-11-11 by Ali - what kind of roof will fit a 60 x 30 foot store?

Good day what type of roof will fit a store 60x30ft and one side of the 60ft is attached to someone house and water is not allowed to slope through it.

On 2020-11-15 - by (mod) -

A flat roof sloped to drain to one or more roof drains that are sized big enough to handle the anticipated water load and that drain to an acceptable location

or

A roof that slopes away from the house you mention

On 2020-10-02 by Christian Luis - simple way to calculate roof height?

Is there any simple way of calculating the roof height?

On 2020-10-02 - by (mod) -

There are several ways to calculate roof height, depending on what access you have to the roof.

See ROOF MEASUREMENTS where we describe all of the methods for measuring roof slope, area, etc.

https://inspectapedia.com/roof/Roof_Measurements.php

We even describe standing on the ground, using a folding ruler, getting the roof angle, and then by making ANY measurement that is accessible, such as building width, you can calculate the roof height.

On 2020-09-22 by Dillon - what will be the slope of my roof?

So I'm trying to figure this out. I'm building a deer shack one post is 6'2 other is 5'7 so that's 7 inches and 6' long so does that mean the slope would be 1.25/12

On 2020-09-22 - by (mod) -

just the roof "drop" between ridge and eaves doesn't give slope: we need the horizontal distance

Dillon:

A 7 inch drop over what horizontal distance? That's how you can calculate the slope.

On 2019-12-24 by Saheed - calculate roof height from building length and width?

My house is 50ft length and 43ft wide. What will be the height of my roof.

On 2020-01-08 - by (mod) -

Saheed,

Given only the length and width of a home we cannot say what it's roof height is. That's a completely different measurement. Take a look at the drawings above on this page.

On 2019-11-24 by aurora - how do you figure out where to sit the roof's ridge board?

when framing a roof, how do you figure out where to sit the roof's ridge board. Like the height of it , i know it goes centered in the house in my case but how high up do you go. My roof is an 8/12 and has a run of 19' 9" .

On 2019-11-25 by (mod) - how do you figure out where to sit the roof's ridge board

Au

Thank you for asking - as the truth is most texts and examples give "theoretical" framing triangle examples to give the ridge height but forget some details that can actually throw that measurement off. I'll try to give a flavor of that here.

An 8 in 12 roof will have 8 inches of vertical rise for each 12 inches of horizontal run.

If your horizontal run is 19.75 ft. (and that'd be for just HALF the total building width if this is a conventional A-shaped gable roof)

then any line you draw: from the top of the outer wall plate, for example,
from the top surface of a rafter where it sits atop the wall plate to the top of the same rafter where it meets the top of the ridge board,

is going to rise 8" (per foot of run) x 19.75 (that's because 19'9" = 19.75 ft) = 158" of total rise or (158/12) 13ft 1.67" from the starting point at the wall top plate.

So the top surface of my ridge board (before any adjustment for the effect of a birds-mouth cut in the rafter at the top plate) is going to be 13.67 ft. above the level of the wall top plate plus the distance from the rafter upper surface to the top plate.

I don't know your rafter size - e.g. 2x8, 2,10, 2x12- so I can't give that additional number.

To be very precise, the carpenter will plan her birds-mouth cut for the seat of rafters at the top plate, and the vertical or plumb cut of that birds-mouth notch will have some height too, for example 1.5".

I like to remember that because if I don't, when I make my birds-mouth cut, the whole rafter, IF I keep the slope unchanged, drops vertically by that same amount, 1.5" - so the top of the ridge drops the same amount.

If you forget this detail then either the slope turns out to be not precisely what you planned or the birds-mouth doesn't sit properly on the top plate.

Other articles in this series are worth a look as we give more examples and calculations

Especially FRAMING TRIANGLES & CALCULATIONS

but also

ROOF SLOPE DEFINITIONS
ROOF MEASUREMENTS where we describe all of the methods for measuring roof slope, area, etc.
ROOF SLOPE TABLE, TYPES, WALKABILITY
STAIR RISE & RUN CALCULATIONS

On 2019-05-08 by Abdu - best slope of traditional tiled house

What is the best slope of traditional tiled house s

On 2019-05-19 by (mod) - What is the best slope of traditional tiled house

Abdu

Please see details at CLAY TILE ROOF SLOPE, DECK & UNDERLAY

There you'll see two roof slope ranges for clay tile roofs; the lower slope range requires a different roofing design and a waterproof underlayment over the whole roof.



...

Continue reading at ROOF SLOPE DEFINITIONS or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see ROOF SLOPE CALCULATION FAQs - questions and answers posted originally on this page.

Or see these

Recommended Articles

Suggested citation for this web page

ROOF SLOPE CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.


Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to BUILDING ROOFING

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Search the InspectApedia website

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Comment Form is loading comments...

Citations & References

In addition to any citations in the article above, a full list is available on request.


ADVERTISEMENT